版本比较
比较
标识
- 该行被添加。
- 该行被删除。
- 格式已经改变。
树的概念
树是一种用于描述一对多的数据结构,比如文件目录结构就可以用树来描述。树的定义如下:
树是n(n≥0)个结点的有限集合,n=0时称为空树,在任意一棵非空树中:
- 有且仅有一个特定的称为根的结点。
- 当n>1时,其余结点可分为m个互不相交的有限集T1,T2,……Tm,每个集合本身又是一棵树,并且称为根的子树。
注意两点,根结点是唯一的,子树互不相交。
二叉树是一种常用的树,它只有两个子结点,除此外多叉树也可能用到,如果一个集合里包含不止一颗树,则称为森林。
树的存储
树的存储分为顺序存储和链式存储。顺序存储是指通过数组来存储树,分为双亲表示法,孩子表示法,双新孩子表示法,如下:
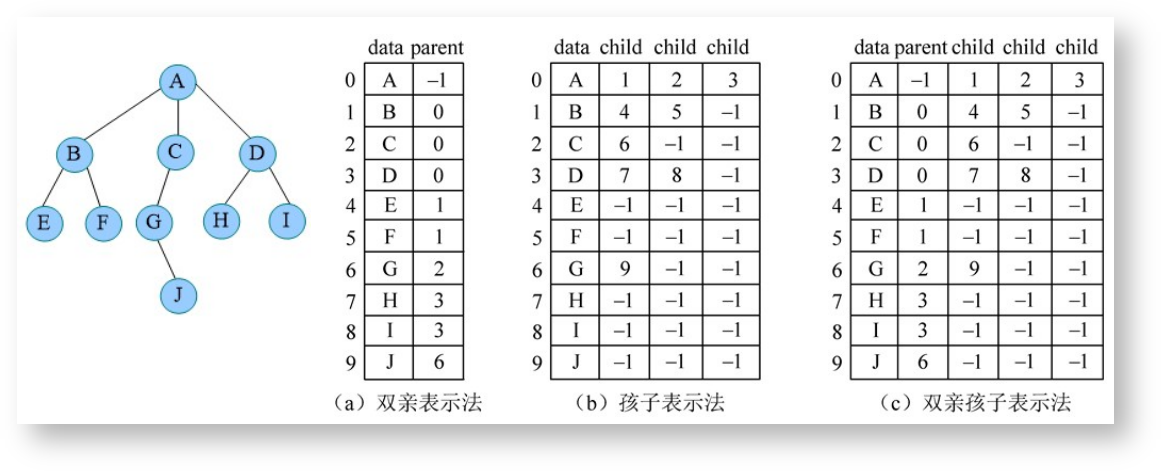 Image Added
Image Added
链式存储使用链表来存储树,分为孩子链表表示法和孩子兄弟表示法,如下:
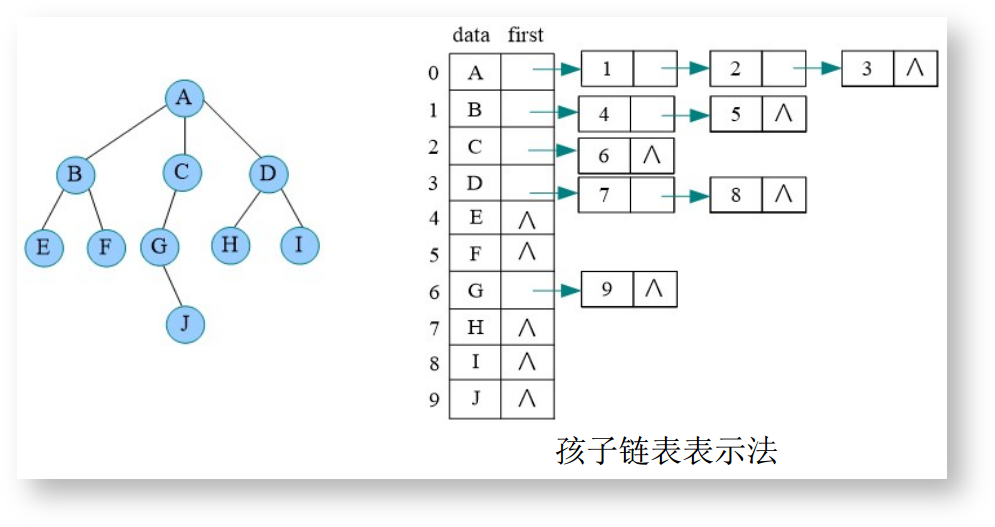 Image Added
Image Added
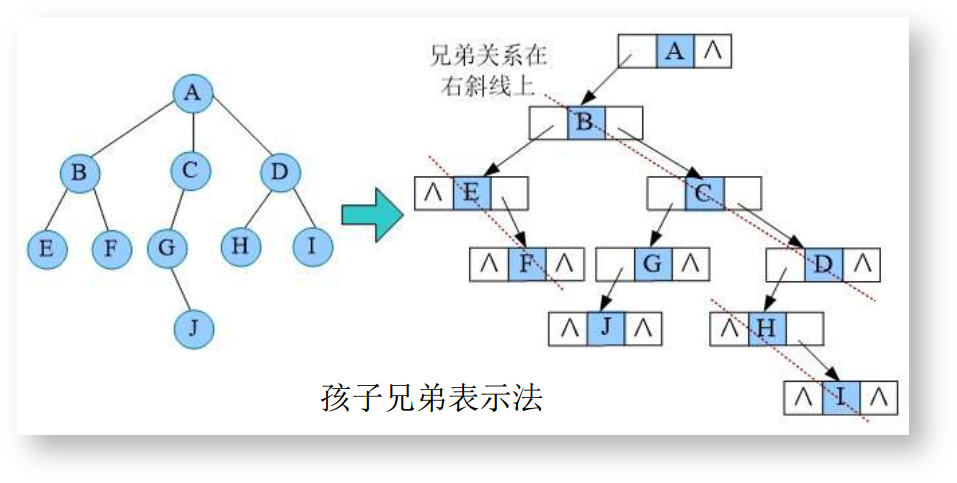 Image Added
Image Added
树的转换
多叉树转换为二叉树
使用孩子兄弟表示法,长子当左结点,兄弟当右结点。
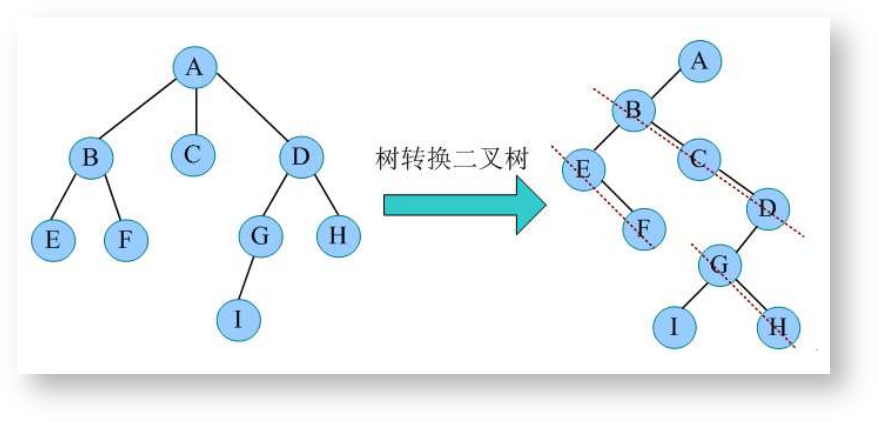 Image Added
Image Added
二叉树还原多叉树
左结点作为长子,右斜线作为兄弟。
 Image Added
Image Added
森林转换为二叉树
把森林中的每棵树的根当成兄弟结点,先把每个树转换成二叉树,然后再将每棵树的根连接在右斜线上。
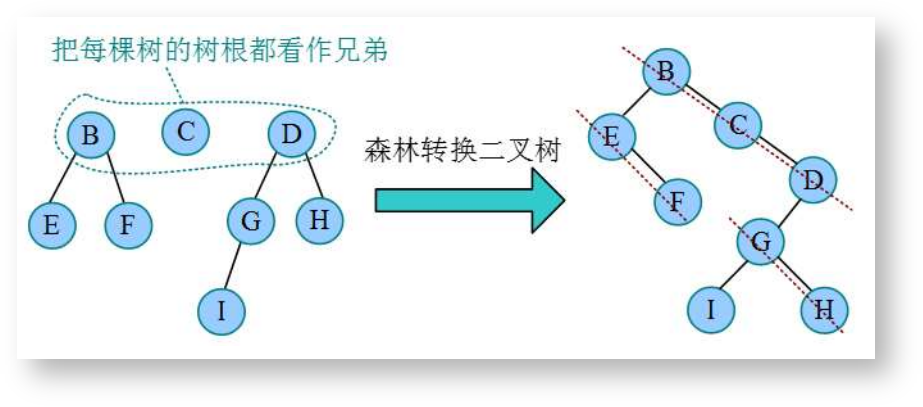 Image Added
Image Added
二叉树还原为森林
右斜线上的每个结点作为一棵树的根,将每棵二叉树还原为树。
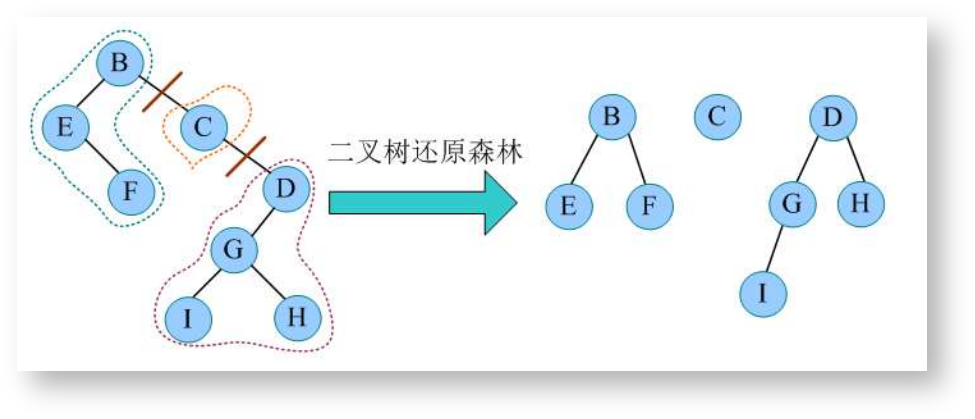 Image Added
Image Added
二叉树性质
- 第k层最多
2k-1个结点。 - k层的二叉树最多
2k-1个结点。 - 对于任何一棵二叉树,若叶子结点数为
n0,度为2的结点数为n2,则n0 = n2 + 1。 - 满二叉树:每一层都填满的二叉树。
- 完全二叉树:除最后一层外,每一层都是满的,最后一层节点从左向右出现。
- 具有n个结点的完全二叉树的深度必为
log2n+1。 - 将完全二叉树按从上下到、从右到右展开到顺序表中,则编号为
i的结点,其左孩子编号必为2i,右孩子编号必为2i+1,其父结点编号必为i/2,应用:- 一颗完全二叉树有1001个结点,其中叶子节点的个数是多少?
- 与之最接近的满二叉树为210-1 = 1023个节点,也就是这个树有10层,前9层的结点数为29-1 = 511个,最后一层的叶子节点为1001-511 = 490个,倒数第二层的叶子结点为29-1 - (490/2) = 11个。
- 一颗完全二叉树第6层有8个叶子,则该完全二叉树最少有几个结点,最多有几个结点?
- 两种情况,一种是第6层是最后一层,这层不满,对应的结点数为前5层满节点加上第6层的8个叶子。第二种情况是第6层为倒数第二层,这层本身是满的,但最后的8个节点没有子结点,对应的结点数是前6层满节点加上第6层8个叶子节点之前的节点的全部叶子。
- 一颗完全二叉树有1001个结点,其中叶子节点的个数是多少?
- 二叉树顺序存储方式:将二叉树的结点按满二叉树的方式进行编号,依次存储到顺序表中。
二叉树遍历
二叉树的遍历按照根、左子树、右子树的访问先后顺序不同,一共有6种访问方案。但实际使用时,一般都固定先访问左子树再访问右子树,在这个前提下,根据根结点的访问顺序,一共有三种访问方案:前序遍历(中-左-右),中序遍历(左-中-右),后序遍历(左-右-中)。
接下来以下面这个二叉树定义来进行遍历:
| 代码块 |
|---|
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
}; |
前序遍历
递归方式:
| 代码块 |
|---|
void preorder(TreeNode *root) {
if(!root) return;
cout << root->val << " ";
preorder(root->left);
preorder(root->right);
} |
非递归方式:
| 代码块 |
|---|
void preorder(TreeNode *root) {
stack<TreeNode*> stk;
TreeNode *cur = root;
while(cur || !stk.empty()) {
while(cur) {
cout << cur->val << " ";
stk.push(cur);
cur = cur->left;
}
cur = stk.top();
stk.pop();
cur = cur->right;
}
} |
中序遍历
递归方式:
| 代码块 |
|---|
void inorder(TreeNode *root) {
if(!root) return;
preorder(root->left);
cout << root->val << " ";
preorder(root->right);
} |
非递归方式:
| 代码块 |
|---|
void inorder(TreeNode *root) {
stack<TreeNode*> stk;
TreeNode *cur = root;
while(cur || !stk.empty()) {
while(cur) {
stk.push(cur);
cur = cur->left;
}
cur = stk.top();
stk.pop();
cout << cur->val << " ";
cur = cur->right;
}
} |
后序遍历
递归方式:
| 代码块 |
|---|
void postorder(TreeNode *root) {
if(!root) return;
preorder(root->left);
preorder(root->right);
cout << root->val << " ";
} |
非递归方式:
| 代码块 |
|---|
void postorder(TreeNode *root) {
stack<TreeNode*> stk;
TreeNode *cur = root;
TreeNode *prev = nullptr;
while(cur || !stk.empty()) {
while(cur) {
stk.push(cur);
cur = cur->left;
}
cur = stk.top();
if(cur->right && cur->right != prev) {
cur = cur->right;
} else {
stk.pop();
cout << cur->val << " ";
prev = cur;
cur = nullptr;
}
}
} |
按层遍历
| 代码块 |
|---|
void levelorder(TreeNode *root) {
if(!root) return;
queue<TreeNode*> q;
q.push(root);
while(!q.empty()) {
int size = q.size();
for(int i = 0; i < size; i++) {
TreeNode *node = q.front();
q.pop();
cout << node->val << " ";
if(node->left) {
q.push(node->left);
}
if(node->right) {
q.push(node->right);
}
}
}
} |
| 目录 |
|---|
...