树的概念
树是一种用于描述一对多的数据结构,比如文件目录结构就可以用树来描述。树的定义如下:
树是n(n≥0)个结点的有限集合,n=0时称为空树,在任意一棵非空树中:
- 有且仅有一个特定的称为根的结点。
- 当n>1时,其余结点可分为m个互不相交的有限集T1,T2,……Tm,每个集合本身又是一棵树,并且称为根的子树。
注意两点,根结点是唯一的,子树互不相交。
二叉树是一种常用的树,它只有两个子结点,除此外多叉树也可能用到,如果一个集合里包含不止一颗树,则称为森林。
树的存储
树的存储分为顺序存储和链式存储。顺序存储是指通过数组来存储树,分为双亲表示法,孩子表示法,双新孩子表示法,如下:
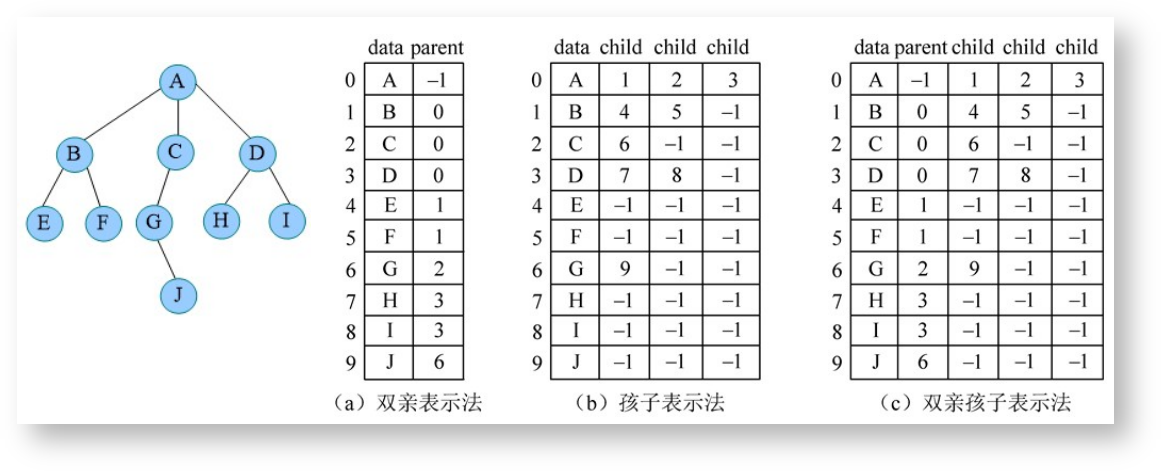
链式存储使用链表来存储树,分为孩子链表表示法和孩子兄弟表示法,如下:
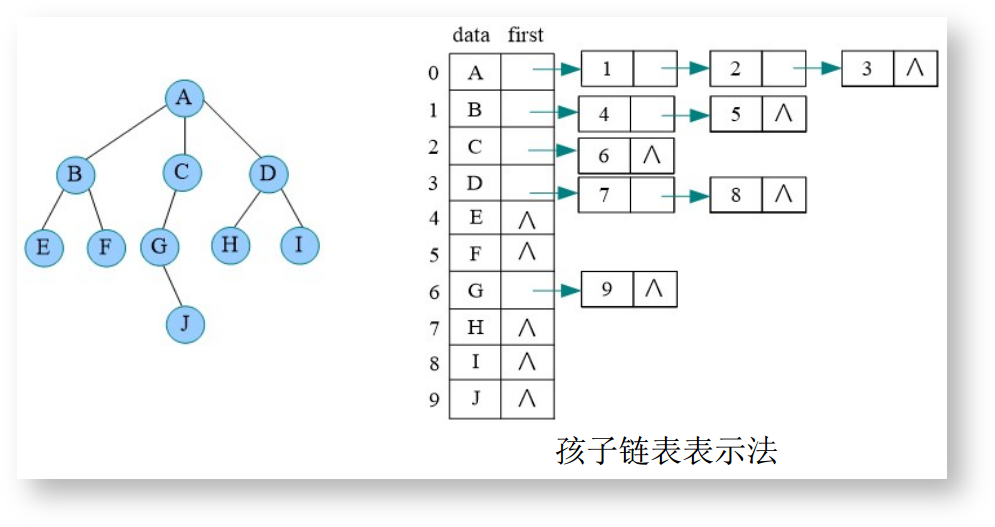
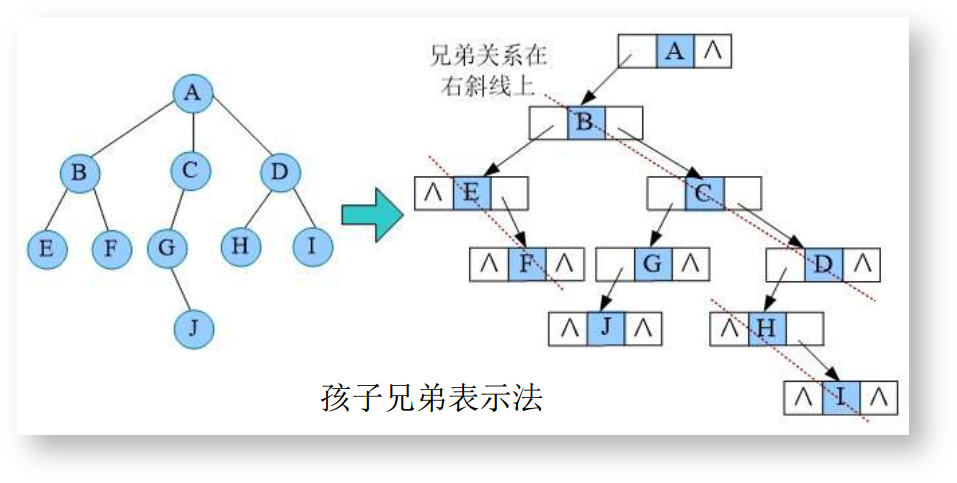
树的转换
多叉树转换为二叉树
使用孩子兄弟表示法,长子当左结点,兄弟当右结点。
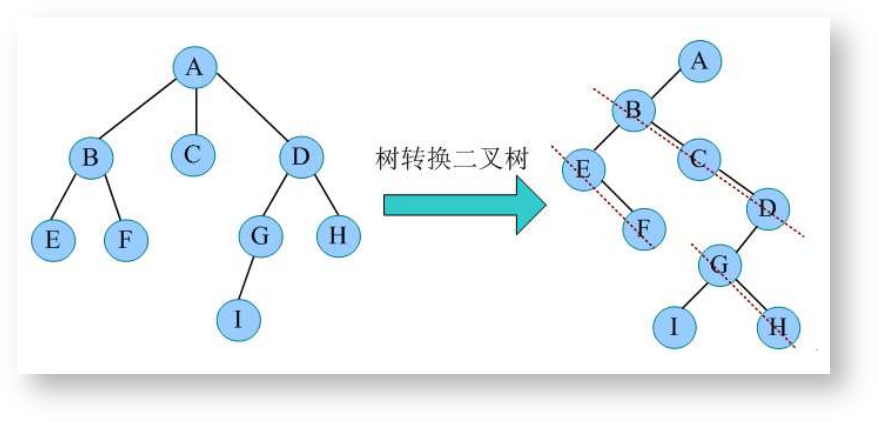
二叉树还原多叉树
左结点作为长子,右斜线作为兄弟。

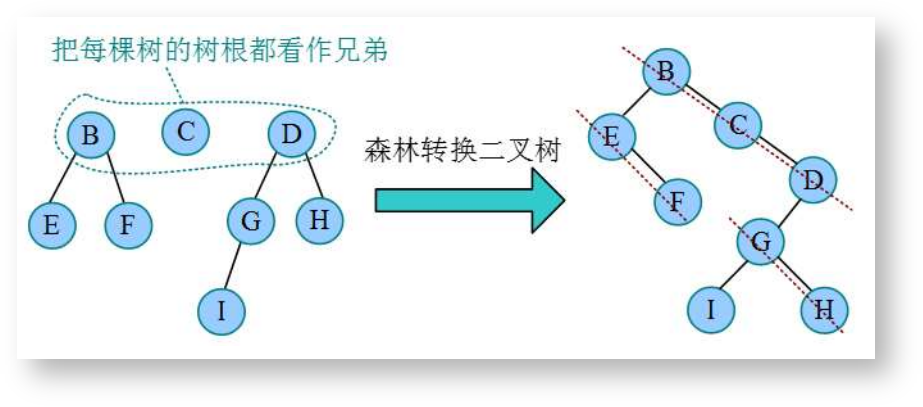
森林转换为二叉树
把森林中的每棵树的根当成兄弟结点,先把每个树转换成二叉树,然后再将每棵树的根连接在右斜线上。
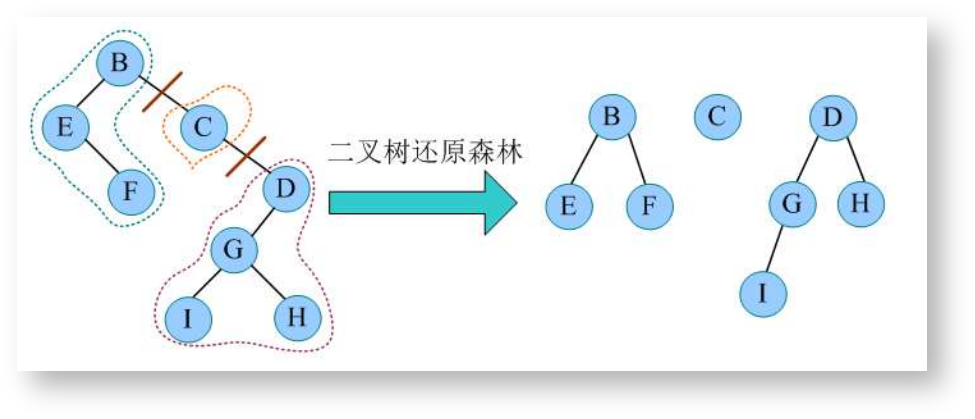
二叉树还原为森林
右斜线上的每个结点作为一棵树的根,将每棵二叉树还原为树。
二叉树性质
- 第k层最多
2k-1个结点。 - k层的二叉树最多
2k-1个结点。 - 对于任何一棵二叉树,若叶子结点数为
n0,度为2的结点数为n2,则n0 = n2 + 1。 - 满二叉树:每一层都填满的二叉树。
- 完全二叉树:除最后一层外,每一层都是满的,最后一层节点从左向右出现。
- 具有n个结点的完全二叉树的深度必为
log2n+1。 - 将完全二叉树按从上下到、从右到右展开到顺序表中,则编号为
i的结点,其左孩子编号必为2i,右孩子编号必为2i+1,其父结点编号必为i/2,应用:- 一颗完全二叉树有1001个结点,其中叶子节点的个数是多少?
- 与之最接近的满二叉树为210-1 = 1023个节点,也就是这个树有10层,前9层的结点数为29-1 = 511个,最后一层的叶子节点为1001-511 = 490个,倒数第二层的叶子结点为29-1 - (490/2) = 11个。
- 一颗完全二叉树第6层有8个叶子,则该完全二叉树最少有几个结点,最多有几个结点?
- 两种情况,一种是第6层是最后一层,这层不满,对应的结点数为前5层满节点加上第6层的8个叶子。第二种情况是第6层为倒数第二层,这层本身是满的,但最后的8个节点没有子结点,对应的结点数是前6层满节点加上第6层8个叶子节点之前的节点的全部叶子。
- 一颗完全二叉树有1001个结点,其中叶子节点的个数是多少?
- 二叉树顺序存储方式:将二叉树的结点按满二叉树的方式进行编号,依次存储到顺序表中。
二叉树遍历
二叉树的遍历按照根、左子树、右子树的访问先后顺序不同,一共有6种访问方案。但实际使用时,一般都固定先访问左子树再访问右子树,在这个前提下,根据根结点的访问顺序,一共有三种访问方案:前序遍历(中-左-右),中序遍历(左-中-右),后序遍历(左-右-中)。
接下来以下面这个二叉树定义来进行遍历:
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
}; |
前序遍历
递归方式:
void preorder(TreeNode *root) {
if(!root) return;
cout << root->val << " ";
preorder(root->left);
preorder(root->right);
} |
非递归方式:
void preorder(TreeNode *root) {
stack<TreeNode*> stk;
TreeNode *cur = root;
while(cur || !stk.empty()) {
while(cur) {
cout << cur->val << " ";
stk.push(cur);
cur = cur->left;
}
cur = stk.top();
stk.pop();
cur = cur->right;
}
} |
中序遍历
递归方式:
void inorder(TreeNode *root) {
if(!root) return;
preorder(root->left);
cout << root->val << " ";
preorder(root->right);
} |
非递归方式:
void inorder(TreeNode *root) {
stack<TreeNode*> stk;
TreeNode *cur = root;
while(cur || !stk.empty()) {
while(cur) {
stk.push(cur);
cur = cur->left;
}
cur = stk.top();
stk.pop();
cout << cur->val << " ";
cur = cur->right;
}
} |
后序遍历
递归方式:
void postorder(TreeNode *root) {
if(!root) return;
preorder(root->left);
preorder(root->right);
cout << root->val << " ";
} |
非递归方式:
void postorder(TreeNode *root) {
stack<TreeNode*> stk;
TreeNode *cur = root;
TreeNode *prev = nullptr;
while(cur || !stk.empty()) {
while(cur) {
stk.push(cur);
cur = cur->left;
}
cur = stk.top();
if(cur->right && cur->right != prev) {
cur = cur->right;
} else {
stk.pop();
cout << cur->val << " ";
prev = cur;
cur = nullptr;
}
}
} |
按层遍历
void levelorder(TreeNode *root) {
if(!root) return;
queue<TreeNode*> q;
q.push(root);
while(!q.empty()) {
int size = q.size();
for(int i = 0; i < size; i++) {
TreeNode *node = q.front();
q.pop();
cout << node->val << " ";
if(node->left) {
q.push(node->left);
}
if(node->right) {
q.push(node->right);
}
}
}
} |