连通分量

相关概念：

连通图：在无向图中，如果图G中任意两个节点都是连通的，则称图G为连通图。

连通分量：无向图G的极大连通子图称为图的连通分量。连通分量可能不止一个，对每个连通分量，如果再向其中加入一个节点，这个子图就不连通。

下图中有几个连通分量？

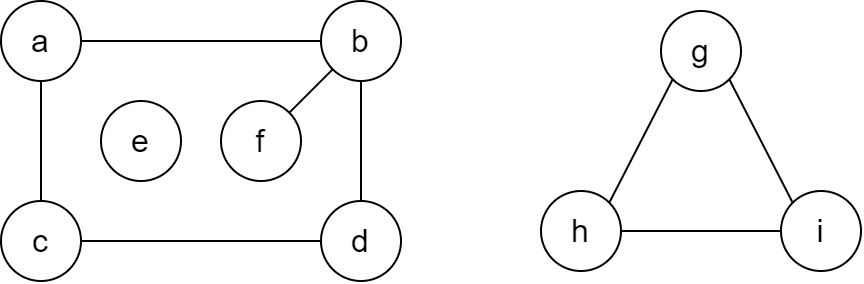
答案：

有3个连通分量，如下图所示，通过不同颜色标记：


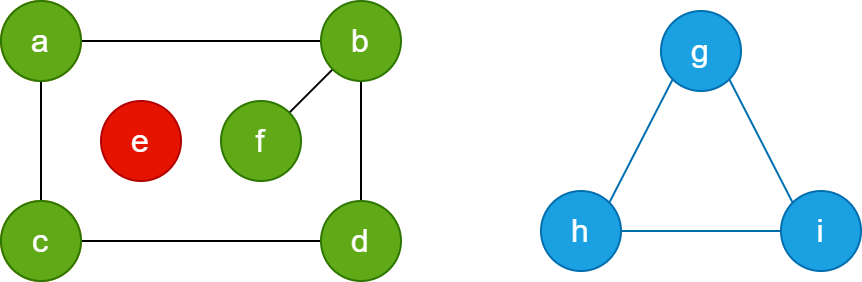
强连通图：在有向图中，如果图中任意两个节点从u到v都有路径，且从v到u也有路径，则称图G为强连通图。

强连通分量：有向图G的极大强连通子图被称为图G的强连通分量。强连通分量也不止一个，对每个强连通分量，如果再向其中加入一个节点，这个子图就不是强连通图。

下图中有几个强连通分量？

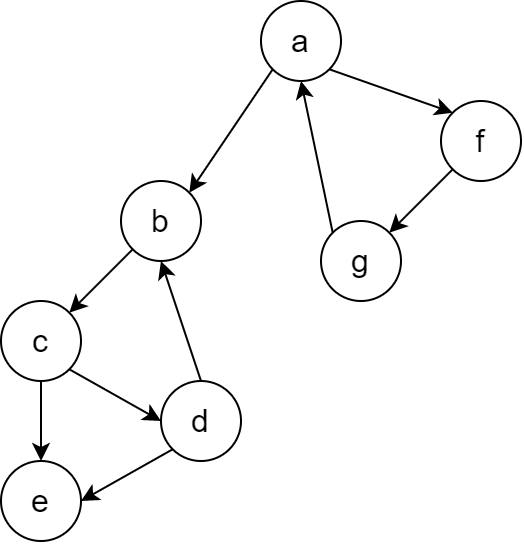
答案：

有3个强连通分量，如下图所示，通过不同颜色标记：


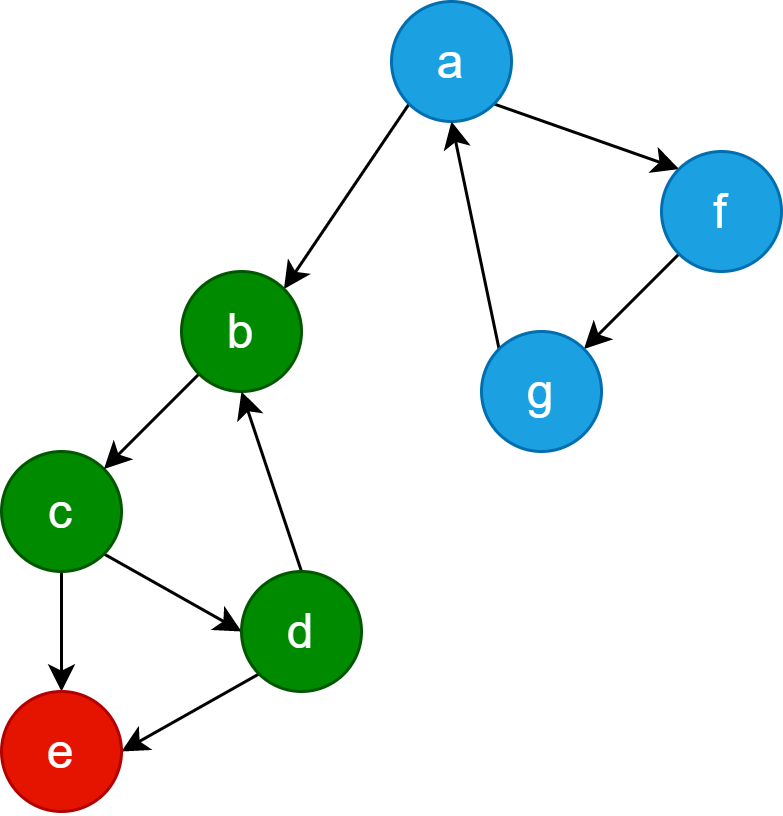
强连通分量求解算法-Tarjan算法模板：

#define MAXN 1005

int G[MAXN][MAXN]; // 邻接矩阵
int n;             // 顶点数，顶点编号从0开始

int timestamp;  // 时间戳
int dfn[MAXN];  // 第一次遍历到达u的时间戳，至少为1，为0表示u还未被访问过
int low[MAXN];  // 从顶点u开始的DFS遍历能到达的最小时间戳

stack<int> stk;
bool in_stk[MAXN]; // 记录顶点u是否在栈中

int scc_cnt;  // 记录强连通分量的个数，也用于给强连通分量编号
int id[MAXN]; // 记录顶点所属的强连通分量编号

void tarjan_dfs(int u) {
    dfn[u] = low[u] = ++timestamp; // 第一次遍历到u，初始化当前点的时间戳
    stk.push(u);
    in_stk[u] = true;
    for(int i = 0; i < n; i++) { // 遍历所有u能到的邻接点
        if(G[u][i]) {
            if(dfn[i] == 0) { // 如果这个点还没被访问过
                tarjan_dfs(i); // 遍历邻接点
                low[u] = min(low[u], low[i]); // 子结点能到的最小时间戳u能也到
            } else if(in_stk[i]) { // 如果这个点还在栈中，说明这个点比u点先访问到，它的时间戳也应该更早
                low[u] = min(low[u], dfn[i]); // 用层级更高的点的时间戳更新u的low值
            }
        }
    }
    if(dfn[u] = low[u]) { // 如果u为某个强连通分量的最高点，则可以输出这个强连通分量
        scc_cnt++; // 连通分量数加1
        int tmp;
        do {
            tmp = stk.top();
            stk.pop();
            in_stk[tmp] = false;
            id[tmp] = scc_cnt; // 标记这个点属于哪个强连通分量
        } while(tmp != u);
    }
}

void tarjan() {
    for(int i = 0; i < n; i++) { // 对所有点进行强连通分量计算
        if(dfn[i] == 0) {
            tarjan_dfs(i);
        }
    }
}


算法大概思路：

  1. DFS遍历所有节点，对每个节点，先访问其全部的邻接点，再访问节点内容。
  2. 记录时间戳，从1开始，按DFS遍历的顺序，每个节点的时间戳依次递增，记为dfn[u]。

  3. 每次访问完一个节点的全部邻接点后，记录从这个节点开始DFS遍历能找到的最小时间戳，记为low[u]。

    dfn[u]：表示第一次遍历到u的时间戳。

    low[u]：表示从点u开始DFS遍历能到达的最小时间戳。

  4. 如果有dfn[u] == low[u]，则说明u是所在强连通分量的最高点，可以把这个强连通分量找出来。


参考链接：

桥与割点

相关概念：

桥：在无向图中，如果去掉图G中的一条边e，图G分裂为两个不相连的子图，那么e就是图G的桥或割边。

割点：在无向图中，如果去掉图G中的一个点v及v关联的所有边，图G分裂为两个或以上不相连的子图，那么v为图的割点。

桥与割点示例：


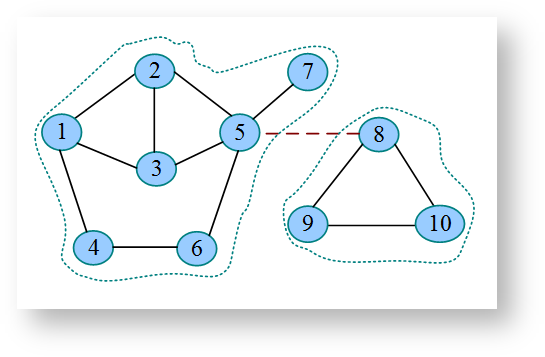
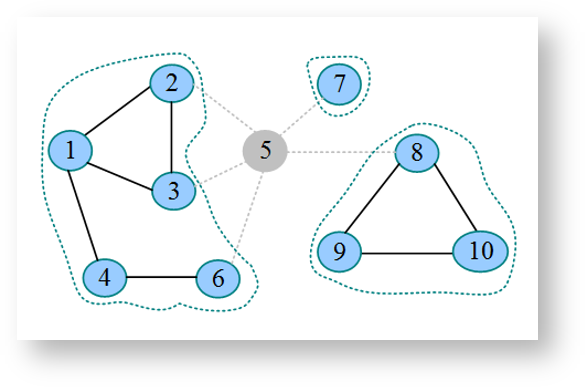
桥与割点的判断：

  1. x是割点case1：x非root节点 && 有子节点 && low[x的子节点] >= dfn[x]。
  2. x是割点case2：x是root节点 && 有>=2个子节点。
  3. x->y是桥：low[y] >= dfn[x]。

了解low[y] >= dfn[x]的含义，如果y是x的子节点，low[y] >= dfn[x]表示从子节点y无法回溯到比x更早的结点，那么从x点断开，子节点y就和x的祖先节点断开了，这就表示x是一个割点，且边x->y是桥。


求桥与割点代码模板：

#define MAXN 1005

int G[MAXN][MAXN]; // 邻接矩阵
int n;             // 顶点数，顶点编号从0开始

int timestamp;  // 时间戳
int dfn[MAXN];  // 第一次遍历到达u的时间戳，至少为1，为0表示u还未被访问过
int low[MAXN];  // 从顶点u开始的DFS遍历能到达的最小时间戳
int fa[MAXN]; // 记录顶点的父节点

bool iscut[MAXN]; // 记录节点是否为割点
bool isbridge[MAXN][MAXN]; // 记录边是否为桥

void tarjan_cut_bridge_dfs(int x) {
    dfn[x] = low[x] = ++timestamp;
    int child = 0;
    for(int y = 0; y < n; y++) {
        if(G[x][y]) {
            if(!dfn[y]) { // y未被访问过
                child++; // x的子结点数加1
                fa[y] = x; // 记录y的父结点为x
                tarjan_cut_bridge_dfs(y);
                if(fa[x] == -1 && child >= 2) { // x是root且有>=2个子结点
                    iscut[x] = true;
                }
                if(fa[x] != -1 && low[y] >= dfn[x]) { // x不是root && x有子结点 && low[y] >= dfn[x]
                    iscut[x] = true;
                }
                if(low[y] >= dfn[x]) { // low[y] >= dfn[x]
                    isbridge[x][y] = true;
                }
                low[x] = min(low[x], low[y]);
            } else if(y != fa[x]) { // y被访问过，且不是x的父结点
                low[x] = min(low[x], low[y]);
            }
        }
    }
}

void tarjan_cut_bridge() {
    for(int i = 0; i < n; i++) { // 初始化全部的顶点的父结点为-1
        fa[i] = -1;
    }
    for(int i = 0; i < n; i++) {
        if(dfn[i] == 0) {
            tarjan_cut_bridge_dfs(i);
        }
    }
}

参考链接：








  • 无标签